广义线性模型（GLM，Generalized Linear Model）

1 理论介绍

1.1 引言

当对数据进行回归分析时，经常会用到两类回归模型：

一类是针对连续型数据进行的线性回归，如下图（图片来源：维基百科）所示

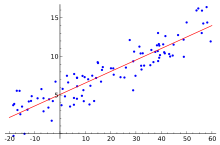
Pasted image 20231114154050.png

这种回归模型的公式是：

y = a_{0} + a_{1} x_{1} + a_{2} x_{2} + \dots + a_{n} x_{n}

还有一类是针对分类数据进行的 logistic 回归，如下图（图片来源）

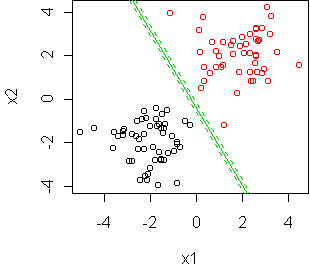
Pasted image 20231114155246.png

y = \frac{1}{1 + e^{- (a_{0} + a_{1} x_{1} + a_{2} x_{2} + \dots + a_{n} x_{n})}}

其中

y = \frac{1}{1 + e^{- x}}

是 sigmoid 函数，可以用来做二分类，其图像如下

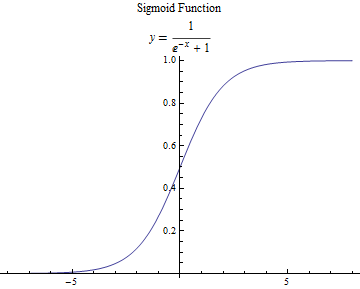
Pasted image 20231114155927.png

Note:数学伎俩——拼凑推广

这两种回归模型，是否有可能统一到一种更加抽象的模型中？这两种形式完全不一样的模型，是不是只是某种更加广义的模型的特例？

1.2 广义线性模型的定义

Define 1 (广义线性模型(Generalized Linear Model)，简称 GLM)

广义线性模型建立在三个定义的基础上，分别为：

定义线性预测算子

η = θ^{T} x

定义 y 的估计值 $h (x, θ) = E (y | x, θ)$
定义 y 的估值概率分布属于某种指数分布族 $f (y | x, θ) = b (y) e x p (η^{T} T (y) - a (η))$

石老师可能有些看不懂？别着急，接下来详细解释各个定义

1.2.1 定义一：线性预测算子

广义线性模型的名字中有『线性』两个字，自然它包含了线性计算的过程，也就是它的假设之一，定义线性预测算子(linear predictor)为：

η = θ^{T} x

这里的 $θ$ 和 $x$ 都是向量，写成标量形式就是：

η = θ_{0} x_{0} + θ_{1} x_{1} + \dots + θ_{n} x_{n}

如果取 $x_{0} = 1$ 。可以发现和

$y = a_{0} + a_{1} x_{1} + a_{2} x_{2} + \dots + a_{n} x_{n}$

是一样的，只是换了一下字母。

1.2.2 定义二：期望估计

先讲一下什么是估计，通常我们需要研究自变量 $x_{0}, x_{1}, \dots, x_{n}$ 与因变量 $y$ 的关系，这些数据可以通过做实验、爬虫获得。可以把通过给定的自变量 $x$ 以及关于研究对象的参数 $θ_{0}, θ_{1}, \dots, θ_{m}$ （可能是先验的，也可能需要通过研究得出）估计因变量 $y$ 的过程，称为“估计”。

Example 1（估计）

现有身高体重数据若干: 比如（180,60），（190,70），（170,80），……
估计身高 200 的人体重是多少
已知身高 $x$ 与体重 $y$ 的关系满足以下分布

f (y | μ, σ) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{(y - μ)^{2}}{2 σ^{2}}}

其中根据世卫组织 $μ = (x － 80) \times 0.7 = 0.7 x - 56$ （自变量 $x$ ，参数 $θ_{0} = - 56, θ_{1} = 0.7$ ）
将 $y$ 的期望作为对 y 的估计，即

h (x, θ) = E (y | x, θ) = μ = 0.7 x - 56 = 0.7 * 200 - 56 = 84

所以估计身高 200 的人体重是 84 kg

Tip

将均值作为估计值是常见的，即

h (x, θ) = E (y | x, θ)

关于估计的理论，之后感兴趣再讲

1.2.3 定义三：指数分布族

可能你已经注意到了，在 example 1 里面，已知某分布

f (y | μ, σ) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{(y - μ)^{2}}{2 σ^{2}}} = \frac{1}{σ \sqrt{2 π}} e^{- \frac{y^{2} - 2 μ y + μ^{2}}{2 σ^{2}}}

而满足分布

f (y | x, θ) = b (y) e x p (η^{T} T (y) - a (η))

的，就满足广义线性分布。

显然 example 1 是满足的， $b(y)=\frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{y {#2} }{2\sigma^2}}$ ，线性预测算子 $η^{T} = μ = 0.7 x - 56$ ， $T (y) = \frac{y}{σ^{2}}$ , $a (μ) = \frac{μ^{2}}{2 σ^{2}}$

指数分布族的性质，见指数分布族。

1 理论介绍

1.1 引言

1.2 广义线性模型的定义

1.2.1 定义一 ：线性预测算子

1.2.2 定义二：期望估计

1.2.3 定义三：指数分布族

1.2.1 定义一：线性预测算子